When should you leave for the bus?
Anyone who has taken the bus has at one time or another wondered, “When should I plan to be at the bus stop?” or more importantly, “When should I leave if I want to catch the bus?” Many bus companies suggest arriving a few minutes early, but there seem to be no good analyses on when to leave for the bus. I decided to find out.
Finding a cost function
Suppose we have a bus route where a bus runs every \(I\) minutes, so if you don’t catch your bus, you can always wait for the next bus. However, since more than just your time is at stake for missing the bus (e.g. missed meetings, stress, etc.), we assume there is a penalty \(\delta\) for missing the bus in addition to the extra wait time. \(\delta\) here is measured in minutes, i.e. how many minutes of your time would you exchange to be guaranteed to avoid missing the bus. \(\delta=0\) therefore means that you have no reason to prefer one bus over another, and that you only care about minimizing your lifetime bus wait time.
Assuming we will not be late enough to need to catch the third bus, we can model this with two terms, representing the cost to you (in minutes) of catching each of the next two buses, weighted by the probability that you will catch that bus:
\[C(t) = \left(E(T_B) - t\right) P\left(T_B > t + L_W\right) + \left(I + E(T_B) - t + \delta\right) P(T_B < t + L_W)\]where \(T_B\) is the random variable representing the time at which the bus arrives, \(L_W\) is the random variable respresenting the amount of time it takes to walk to the bus stop, and \(t\) is the time you leave. (\(E\) is expected value and \(P\) is the probability.) We wish to choose a time to leave the office \(t\) which minimizes the cost function \(C\).
If we assume that \(T_B\) and \(L_W\) are Gaussian, then it can shown that the optimal time to leave (which minimizes the above function) is
\[t = -\mu_W - \sqrt{\left(\sigma_B^2 + \sigma_W^2\right)\left(2\ln\left(\frac{I+\delta}{\sqrt{\sigma_B^2+\sigma_W^2}}\right)-2\ln\left(\sqrt{2\pi}\right)\right)}\]where \(\sigma_B^2\) is the variance of the bus arrival time, \(\sigma_W^2\) is the variance of your walk, and \(\mu_W\) is expected duration of your walk. In other words, you should plan to arrive at the bus stop on average \(\sqrt{\left(\sigma_B^2 + \sigma_W^2\right)\left(2\ln\left(\left(I+\delta\right)/\sqrt{\sigma_B^2+\sigma_W^2}\right)-2\ln\left(\sqrt{2\pi}\right)\right)}\) minutes before your bus arrives.
Note that one deliberate oddity of the model is that the cost function does not just measure wait time, but also walking time. I optimized on this because, in the end, what matters is the total time you spend getting on the bus.
What does this mean?
The most important factor you should consider when choosing which bus to take is the variability in the bus’ arrival time and the variability in the time it takes you to walk to the bus. The arrival time scales approximately linearly with the standard deviation of the variability.
Additionally, it scales at approximately the square root of the log the your value of time and of the frequency of the buses. So even if very high values of time and very infrequent buses do not substantially change the time at which you should arrive. For approximation purposes, you might consider adding a constant in place of this term, anywhere from 2-5 minutes depending on the frequency of the bus.
Checking the assumption
First, we need to collect some data to assess whether the bus time arrival (\(T_B\)) is normally distributed. I wrote scripts to scrape data from Yale University’s Blue Line campus shuttle route. Many bus systems (including Yale’s) now have real-time predictions, so I used many individual predictions by Yale’s real-time arrival prediction system as the expected arrival time, simulating somebody checking this to see when the next bus comes.
For our purposes, the expected arrival time looks close enough to a Gaussian distribution:
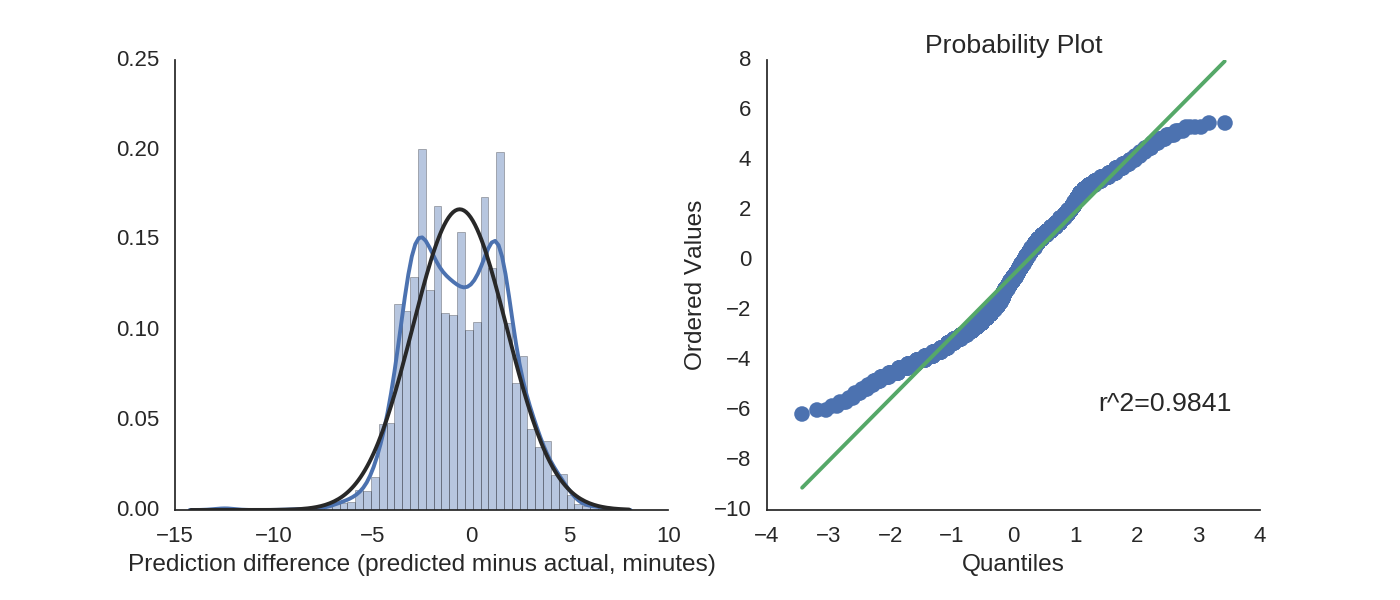
It actually looks like a Gaussian!
So what time should I leave?
When estimating the \(\sigma_B^2\) parameter, we only examine bus times which are 10 minutes away or later. This is because you can’t use a real-time bus system to plan ahead of time to catch something if it is too near in the future, which defeats the purpose of the present analysis. The variance in arrival time for the Yale buses is \(\sigma_B^2=5.7\).
We use an inter-bus interval of \(I=15\) minutes.
While the variability of the walk to the bus station \(\sigma_W^2\) is unique for each person, I consider two cases: one case, where we assume that arrival time variability is small (\(\sigma_W^2=0\)) compared to the bus’ variability, representing the case where the bus stop is (for intance) located right outside one’s office building. I also consider the case where the time variability is comperable to the variability for the bus (\(\sigma_W=5\)), representing the case where one must walk a long distance to the bus stop.
Finally, I consider the case where we strongly prioritize catching the desired bus (\(\delta=60\) corresponding to, e.g., an important meeting) and also the case where we seek to directly minimize the expected wait time (\(\delta=0\) corresponding to, e.g., the commute home).
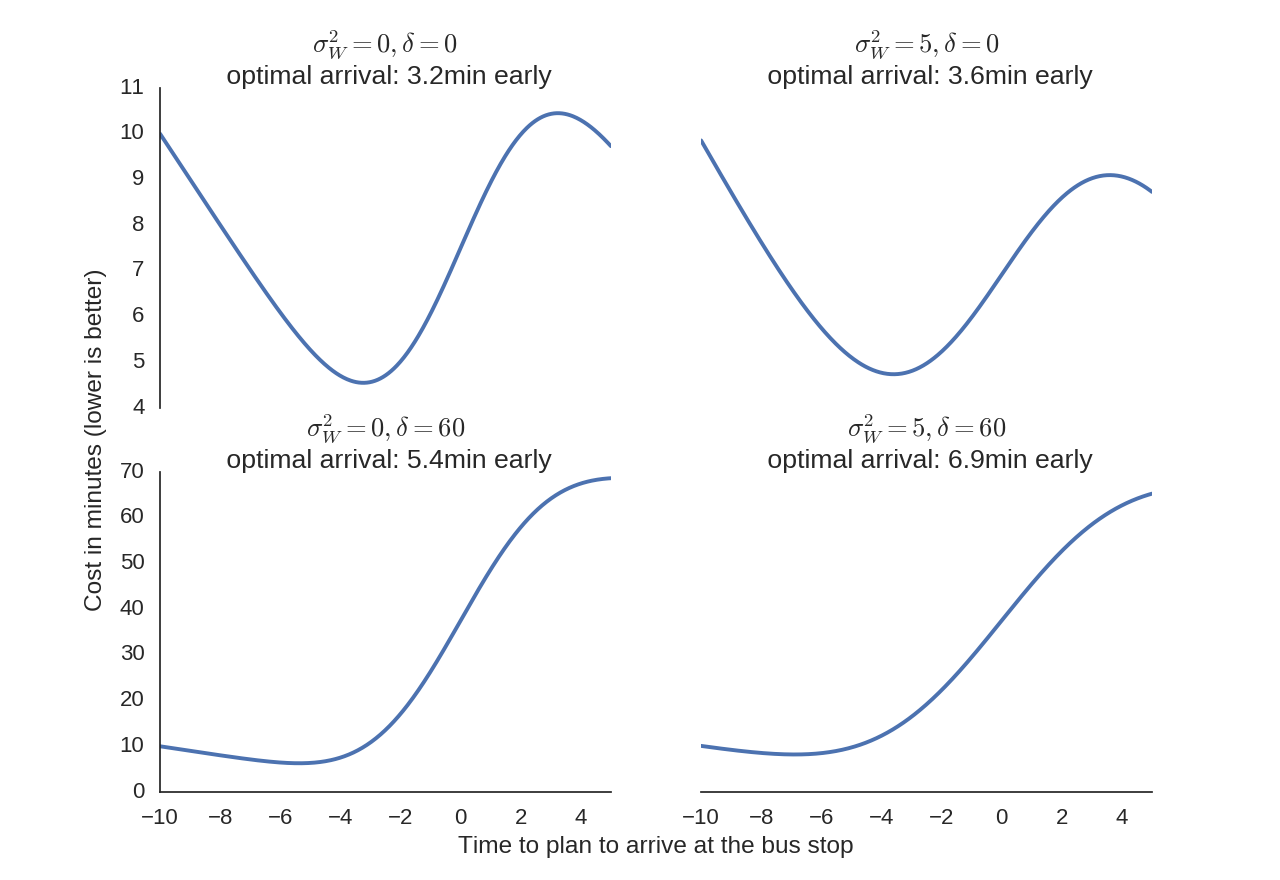
Even though the shape of the optimization function changes greatly, the optimal arrival time changes very little.
We can also look at a spectrum of different cost tradeoffs for missing the bus (values of \(\delta\)) and variance in the walk time (values of \(\sigma_W^2 = var(W)\)). Because they appear similarly in the equations, we can also consider these values to be changes in the interval of the bus arrival \(I\) and the variance of the bus’ arrival time \(\sigma_B^2=var(B)\) respectively.
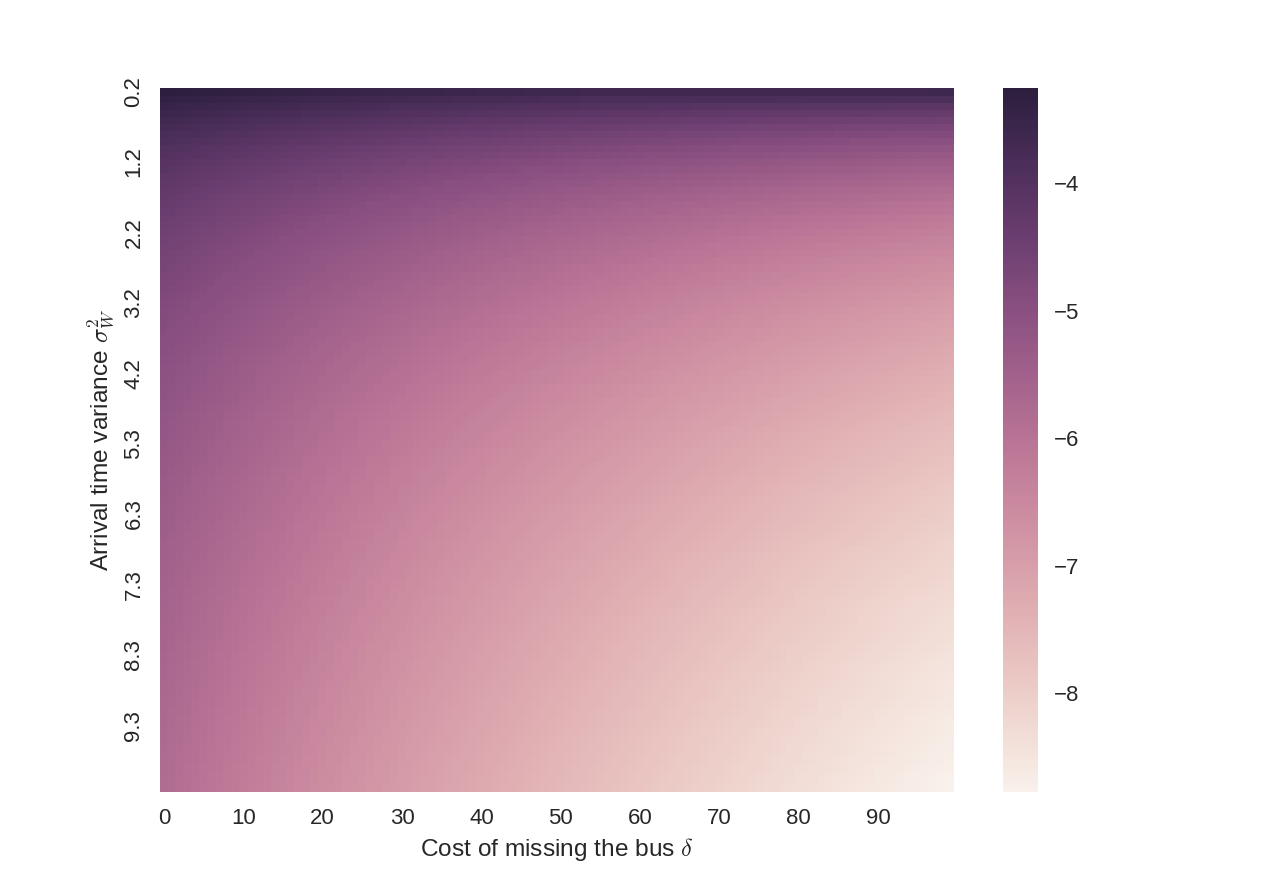
Across all reasonable values, the optimal time to plan to arrive is between 3.5 and 8 minutes early.
Conclusion
So to summarize:
- If it always takes you approximately the same amount of time to walk to the bus stop, plan to be there 3-4 minutes early on your commute home, or 5-6 minutes early if it’s the last bus before an important meeting.
- If you have a long walk to the bus stop which can vary in duration, plan to arrive at the bus stop 4-5 minutes early if you take the bus every day, or around 7-8 minutes early if you need to be somewhere for a special event.
- These estimations assume that you know how long it takes you on average to walk to the bus stop. As we saw previously, if you need to be somewhere at a certain time, arriving a minute early is much better than arriving a minute late. If you don’t need to be somewhere, just make your best guess.
- The best way to reduce waiting time is to decrease variability.
- These estimates also assume that the interval between buses is sufficiently large. If it is small, as in the case of a subway, there are different factors that govern the time you spend waiting.
- This analysis focuses on buses with an expected arrival time, not with a scheduled arrival time. When buses have schedules, they will usually wait at the stop if they arrive early. This situation would require a different analysis than what was performed here.