Does “Flight of the Bumblebee” resemble bumblebee flight?
Flight of the Bumblebee is one of the rare pieces of classical music which, through its association with bees, has cemented its place in pop culture. However, it is unclear whether its composer, Nikolai Rimsky-Korsakov, actually took inspiration from bumblebee flight patterns. I address this question using new tools from ethology, mathematics, and music theory. Surprisingly, the melody line of ``Flight of the Bumblebee’’ mimics a distinctive property of bumblebee flight, a property which was not formally discovered until decades after Rimsky-Korsakov’s death. Therefore, yes, it is very likely1 that Rimsky-Korsakov observed and incorporated actual bumblebee flight patterns into his music.
In what follows, I assume the reader has a knowledge of high school level mathematics and basic music theory (chord changes, intervals, scales, etc.). This post is based on my recent preprint, available on SocArXiv.
Historical background
The piece we now call “Flight of the Bumblebee” actually comes from one of Rimsky-Korsakov’s operas, “The Tale of Tsar Saltan”. The opera is based on a story by Alexander Pushkin, which is in turn based on several folk tales. The hero, Prince Gvidon, is cast on a remote island by his jealous aunts. While there, he unknowingly saves a Swan Princess from death, so in return, she looks after his well-being. To help him to see his father again, she temporarily transforms him into a bee2 so he may fly back to the kingdom (and sting his aunts). Eventually, when he is a human again, Prince Gvidon is reunited with his father and marries the swan princess.
Flight of the Bumblebee begins towards the end of the first scene of Act III after Prince Gvidon is transformed into a bee. The first half of the piece serves as background music for the Swan Princess’ singing as Prince Gvidon flies away. The second half serves as a transition from the first to second scene of Act III. In most renditions of this piece today, the Swan Princess’ vocal line is removed. The piece introduces the “bumblebee” theme, which continues to be a central theme of Act III as Prince Gvidon flies around the court causing mischief.
Despite the fact that Flight of the Bumblebee is by far the most recognisable piece of music Rimsky-Korsakov wrote in his lifetime, he didn’t consider it to be one of his major works. In fact, Rimsky-Korsakov didn’t even include it in his own suite of highlights from the opera3. This piece was relatively unknown until 1936, when it first4 entered pop culture as the theme song for the radio show “The Green Hornet”. It only took a few years to become widely recognisable, in large part due to a 1941 big band jazz cover by Harry James.
Bumblebee flight
In accordance with the cliché “busy as a bee”, bumblebees spend most of their day looking for food. So, we can understand bumblebee flight patterns by understanding how they forage for food. New miniature radar technology allows us to track the flight of foraging bumblebees. One important characteristic aspect we have discovered about insect foraging flight patterns, and bumblebee flight in particular, is the presence of lots of short movements and a few very large movements. At any given point in time, a bee may choose to move in any direction it wants. Most of the time, it will move a small distance. However, sometimes, it will make very large movements. For example, it may travel long distances and then carefully explore a small patch. Relatively speaking, bees will make fewer moderate-sized movements: most movements will be very small, but those which aren’t small will be very large. This has been shown to be optimal behaviour for bumblebees in many situations. In fact, algorithms inspired by this bumblebee behaviour have been used to tackle complex engineering challenges. This type of movement is in contrast to, e.g., the movement of spores released from trees, which tend to drift gently with the wind and not make large, sudden movements across a pasture. We will refer to these large movements as “jumps”.
If you think about it, it makes sense why bees might prefer to sometimes make very large movements when they are searching for food. If they always take small steps, they may never get to the large food source that is on the other side of the meadow. Indeed, this strategy is used by a wide range of animals beyond bumblebees5.
Mathematical analysis of bumblebee flight
To represent these flight patterns, we need to build an extremely simple model which is easy to work with and can be applied to a melody line. First, we need a way to relate the notes in a melody line to the location of a bee. One natural way is to assume that the ups and downs of the melody line correspond to movements of the bee. We can do this by assigning a numerical value to each note in the melody line, where 0 is the lowest note on the piano keyboard and each half step interval is 1 higher than the previous. Then, tracking the note in the melody line is the same as tracking the location of the bee. With this representation, a small movement for a bee is equivalent to a small interval in the melody line. Likewise, a “jump” for the bee is analogous to a “jump” in the melody line, or a large interval.
Now we can think about how a simple bumblebee flight model might operate. The “small steps and large jumps” behaviour we described in the previous section depends only on the sizes of the steps the bee takes at subsequent points in time, not on the direction. So without making assumptions about the direction of each step, we can specify the probability of having steps of different sizes. Then, we can assume that the bee goes in a random direction at each step. This model, known as a random walk, is used to model a huge number of phenomena in the natural world.
We will compare two models for choosing our step sizes in the random walk6. The first, the “geometric” model, is a good representation for most types of data. It posits that steps become proportionally less frequent as they get larger. So, if 50% of steps are of size 1, 25% will be of size 2, 12.5% will be of size 3, and so on. This means that large step sizes are extremely infrequent: if we continue the pattern forward, a step size of one octave (12) will only occur once every 4000 steps, and a step of two octaves (24) will occur once every 16 million steps!
By contrast, we can also use a “powerlaw” model for step sizes. Here, the probability of having a step of a given size is proportional to a power of the size of the step. This is harder to do in our head, so I worked out these numbers for us: if 50% of steps are of size 1, then only 15% of steps are of size 2, and 7% are of size 3. But, if we go out to larger steps, a one-octave jump will occur once every 146 steps, and a two octave jump will occur once every 485 steps! So, compared to the geometric model, the powerlaw model allows large jumps to happen much more frequently, with relatively fewer medium-sized jumps. Both of these models have only one parameter, describing the scale on which they operate.
Here is a simulation of what a bumblebee’s flight path might be under each model.
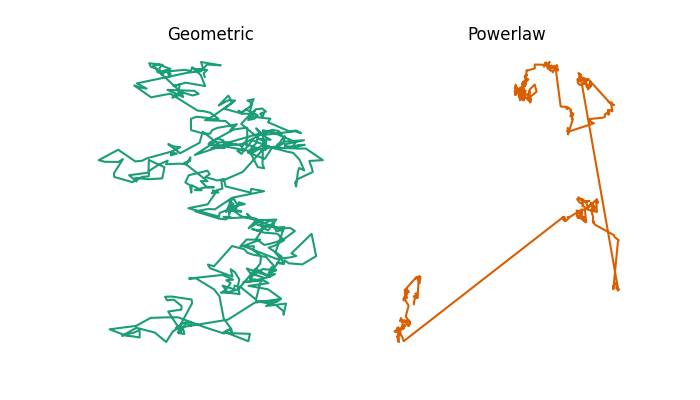
Example 2-dimensional flight trajectories from a geometric or powerlaw random walk model.
As you can see, the powerlaw model involves several large jumps, whereas the geometric model doesn’t. You can compare this to some example bumblebee flight trajectories measured by Juliet Osborne and colleagues, which show patterns which more closely resemble the powerlaw model than the geometric model.
While bumblebees fly in three dimensions, our melody line is only measured in one dimension. So, we need to convert these models into one dimension in order to compare them to Flight of the Bumblebee. First, let’s simulate these models and compare them to the actual melody line. These simulations try to match the qualitative character of the jumps of the melody line, rather than the exact “flight path” of the melody line. Here are example flight paths from the one-dimensional versions of these models, as well as the one derived from the melody of Flight of the Bumblebee:
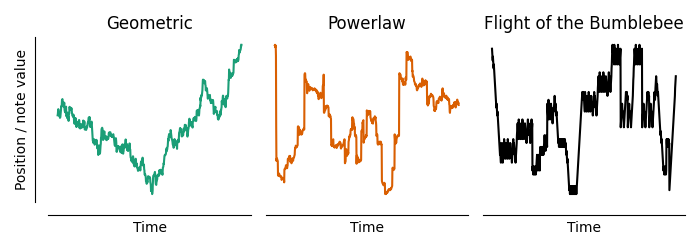
Example 1-dimensional “flight” trajectories from a geometric or powerlaw random walk model, compared to the melody line from Flight of the Bumblebee.
The melody line appears to have a more similar “jumpiness” to the powerlaw model than the geometric model. We can formalise this by fitting the models directly to the jump sizes in melody line (through maximum likelihood, see the appendix on methods for details), and then evaluating the fit to see which model is more likely given the data. When we do so, we find that the powerlaw model is \(1.5 \times 10^{72}\) times more likely than the geometric model!
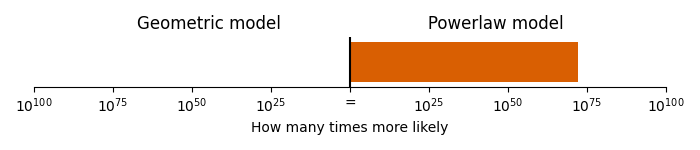
Comparison of geometric and powerlaw model.
This gives us very, very strong evidence that the Flight of the Bumblebee follows a pattern involving small steps and large jumps, over a pattern with a more balanced distribution of small and medium sized jumps.
Control analysis
Flight of the Bumblebee is based on the chromatic scale, and the chromatic scale contains lots of small intervals. Is it possible that this correspondence to the powerlaw model is just due to the extensive use of the chromatic scale? To test this, we can perform the same analysis on the other7 highly-chromatic piece of classical music widely known in pop culture: Entry of the Gladiators by Fučík (i.e., the circus song). Entry of the Gladiators also contains lots of chromatic passages and several large jumps. However, in stark contrast to Flight of the Bumblebee, given the melody line in Entry of the Gladiators, the geometric model was 1.8 times more likely than the powerlaw model.
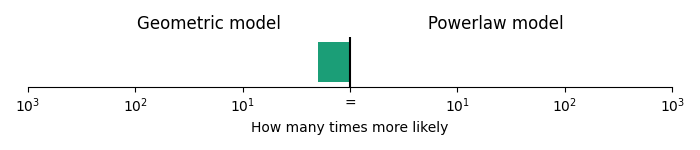
Comparison of geometric and powerlaw model on Entry of the Gladiators.
This means that not all music based on the chromatic scale follows powerlaw step sizes.
At first, it may come as a surprise that Entry of the Gladiators isn’t better fit by powerlaw model. Like Flight of the Bumblebee, it also has lots of small intervals and lots of large jumps. In fact, it has far more large jumps than Flight of the Bumblebee. The reason it is not better fit is because Entry of the Gladiators also contains several intermediate-sized jumps. These intermediate-sized jumps aren’t predicted by the powerlaw model or by models of bumblebee flight. Flight of the Bumblebee contains almost exclusively chromatic steps and large jumps, which makes the powerlaw model a better fit. This means that Flight of the Bumblebee bears more of a mathematical resemblance to the behavioural patterns of bumblebee flight than this other highly-chromatic piece.
What did Rimsky-Korsakov intend to write?
These analyses raise an important question: is there a music theory explanation for including large jumps beyond the imagery of bumblebee flight? Likewise, which aspects of the piece are intended to invoke the imagery and which are incorporated for other musical or artistic purposes?
We know that Rimsky-Korsakov didn’t explicitly implement these mathematical models in his music. Not only was there scarce knowledge about insect behaviour when the Tale of Tsar Saltan premiered in November 1900, but the mathematics on which the models are based hadn’t even been invented yet! In order to make a judgement about step sizes in the melody line, we first must understand what musical and artistic aspects influenced the melody line. Let’s explore two here: the hero’s main theme, and the use of the whole-tone scale.
Hero’s main theme
One important component of the melody line is the hero Prince Gvidon’s theme8 (leitmotif) within the opera. This theme comes from the folksong “Заинька Попляши” (“Zainka Poplyashi”, which roughly translates to “Dance, bunny, dance!”), a song with which Rimsky-Korsakov was intimately familiar. The theme is:
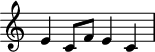
Leitmotif of Prince Gvidon’s.
As you can see below, the character’s theme is clearly represented in main bumblebee melody line, as indicated by red note heads:

Melody line of Flight of the Bumblebee with highlighted leitmotif.
What this means is that one of the most common jumps, the jump of a perfect 4th in the main theme, can be “explained” by this theme. Since the frequency and size of jumps is critical in our mathematical analysis, we can repeat the analysis while ignoring these specific jumps in the melody line. As we see, doing so doesn’t ruin the mathematical effect described in the previous section: the powerlaw model is \(1.8 \times 10^{65}\) times more likely, given the melody line.
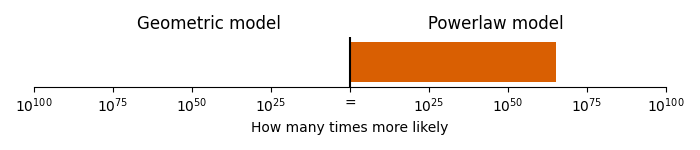
Comparison of geometric and powerlaw model.
So, the use of perfect 4th jumps to capture Gvidon’s leitmotif isn’t a major factor in what makes this melody resemble bumblebee flight.
Whole-tone scale
The piece also has a close connection with the whole-tone scale. While the whole-tone scale is most closely associated today with the French impressionists like Debussy and Ravel, it was actually used much earlier by Rimsky-Korsakov’s contemporaries as a building block of Russian nationalistic music. In this school of music, the whole-tone scale is used to represent the magical, the regal, the ominous, and the surreal.
Given the magical nature of a human transforming into a bumblebee, it may come as no surprise that the whole-tone scale plays a prominent role in Flight of the Bumblebee. Recall that there are only two whole-tone scales, which contain no notes in common.

The two whole-tone scales.
Since the scales contain no notes in common, we can classify any given note as belonging to one of the two whole-tone scales.
In Flight of the Bumblebee, almost all of the pitches on the eighth note beats fall into the C♮ whole-tone scale, and all of the notes on the off-beats fall into the D♭ whole-tone scale. This trend is only violated five times. In three cases, the piece modulates from A minor to D minor (the subdominant), when the whole-tone scales switch. One violation is to make the melody line align properly at the repeat9, and the final violation is to make sure the final note of the piece falls on A, the tonic.
We can visualise this by plotting each on-beat in the melody line of the piece. The x axis indicates the time at which each note is played, and the y axis indicates which whole-tone scale the note comes from. If we show the entire piece in one plot, the on-beats look like this:

The whole-tone scale associated with each on-beat in Flight of the Bumblebee. Individual points appear as lines because they are very close together in time.
And the off-beats look like this:

The whole-tone scale associated with each off-beat in Flight of the Bumblebee. Individual points appear as lines because they are very close together in time.
There aren’t very many switches between whole-tone scales, and those that do occur have a clear musical purpose. This appears to be a deliberate use of the whole-tone scale in the piece.
An objection one might make to this is that the whole-tone scale is by necessity connected with the chromatic scale. Since Flight of the Bumblebee uses the chromatic scale, this property of the whole-tone scale might arise naturally.
To show this objection doesn’t apply, we can perform the same analysis on Entry of the Gladiators. Here, unlike in Flight of the Bumblebee, we see no deliberate use of whole-tone scale for the on-beats:

The whole-tone scale associated with each on-beat in Entry of the Gladiators.
Or for off-beats:

The whole-tone scale associated with each off-beat in Entry of the Gladiators.
This means that the whole-tone scale seems to have been deliberately used by Rimsky-Korsakov, but not by Fučík, in constructing the melody line.
Interestingly, this pattern makes it more “difficult” to write a melody line which includes large jumps. This is because large jumps can only be included if they sound nice. It is musically “easy” to maintain the whole-tone scale pattern while making medium-sized jumps, because most medium-sized jumps sound pleasant in many different contexts. All intervals from minor 2nds to major 6ths are extremely common across a wide range of musical genres. By contrast, it is more difficult to make large jumps sound nice. In most pieces, large jumps often occur at octave, 9th, 10th, or flat 7th intervals, all of which would violate the alternating whole-tone scale pattern. This means that the use of the whole-tone scale in the melody line actually makes it more difficult to have large jumps. So, because of the whole-tone scale pattern, the presence of large jumps in Flight of the Bumblebee is even more surprising than the mathematical analysis suggests.
Rimsky-Korsakov also left out some medium-sized jumps which fit the whole-tone scale pattern. Another “valid” jump under the whole-tone pattern, and one which is extremely common in other pieces, is the perfect 5th. However, the perfect 5th, a medium-sized jump, only occurs once in the melody line of Flight of the Bumblebee. Two similarly “easy-to-use” intervals which satisfy the whole-tone pattern, the minor 3rd and the major 6th, don’t occur at all. The only medium-sized interval that Rimsky-Korsakov uses is the perfect 4th, which we already showed was a result of Prince Gvidon’s theme. So, the use of large jumps and not medium sized jumps appears to be a deliberate choice by the composer.
Conclusion
Flight of the Bumblebee is a much more musically complex piece than it initially seems. Rimsky-Korsakov appears to have deliberately mimicked an important property of bumblebee flight within his music. Mathematical models to describe bumblebee flight, invented long after Rimsky-Korsakov’s time, end up providing an excellent fit to his melody line. On top of this, he incorporated interesting features from a music theory perspective, including the main character’s theme and a whole-tone scale pattern. These musical features don’t explain the melody line’s resemblance to bumblebee flight. While we will never know if Rimsky-Korsakov actually observed bumblebee flight while composing Flight of the Bumblebee, it sure is fun to speculate10, isn’t it?
Appendix: Methods
To find the melodic pattern, I downloaded Nicolas Froment’s engraving of the Rachmaninoff piano arrangement and cut out everything except the melody line. Then, I cross-referenced this to the score from the original opera, page 262-267, to tweak the melody line to ensure it is faithful to that of the opera rather than the piano arrangement, correcting for octaves, breaks, repeats, etc. I exported this as MIDI (attached below) and analysed it using a Python script (attached below). Likewise, I used James Birgham’s engraving of the piano reduction of Entry of the Gladiators and exported to MIDI (attached).
I only used sections of Flight of the Bumblebee which were part of the rapid, recognisable melody, concatenating across breaks. Likewise, I excluded the trio section of Entry of the Gladiators since it isn’t based on chromatics. Repeated notes were excluded since a jump of zero in a discrete random walk doesn’t correspond to any kind of step in a continuous Wiener or Levy process. I adjusted the octave down in two cases (penalising the powerlaw model): once for a two-octave jump in the final run of Flight of the Bumblebee, since it was an artistic flourish for the finale; and once for a two-octave jump when the melody line switches from treble to bass in Entry of the Gladiators.
Model fitting was performed by finding the pairwise distances between neighbouring points in each timeseries, and then fitting the counts of each to a geometric or Zipf distribution through maximum likelihood. A numerical minimisation routine was used to find parameters which maximised the likelihood function.
The music theory analysis was partially my own (whole-tone scale analysis) and partially based on work from Rosa Newmarch, Victoria Williams and John Nelson (historical and motivic analysis). Thank you to Sophie Westacott for helpful comments, and to the giant bumblebee who regularly hovers outside my window and then darts away for inspiration.
Code/Data:
- Analysis script
- Script to generate plots
- Flight of the Bumblebee MIDI melody
- Entry of the Gladiators MIDI melody
Footnotes
-
contrary to Betteridge’s law ↩
-
In the Pushkin story, he was also transformed into a mosquito and a fly to see his father and sting his aunts, for a total of three trips back. ↩
-
Due to the piece’s broad recognisability today, many orchestras insert Flight of the Bumblebee into the suite anyway. ↩
-
Contrary to claims from some sources, it didn’t appear in Charlie Chaplin’s 1925 film “Gold Rush” - instead, it appeared in the 1942 version, which used different music. ↩
-
Similarly, when humans seek food, it is occasionally wise to take a large step and go to the supermarket instead of always looking inside the refrigerator. ↩
-
As a technical note: ideally, we would want to consider the difference between a Wiener process (Brownian motion) and a Levy process, which is similar to Brownian motion except the steps are powerlaw-distributed. Since our melody line is discrete in pitch (i.e. there are only 12 notes per octave), we must use a model with discrete steps in order to get a likelihood which makes sense. So, we use the geometric distribution and the discrete powerlaw distribution (zeta or Zipf distribution). We use the geometric distribution as a stand-in for the normal distribution, since there is no well-known discrete half-normal–like distribution with support on all the natural numbers. ↩
-
The use of “the” was deliberate. I don’t think there are any other pieces of classical music which are widely known in pop culture and rely so heavily on chromatics. The internet doesn’t seem to think so either, but please correct me if I am wrong! (Habanera from Carmen doesn’t count, since it only embeds a descending chromatic scale within a surrounding not-so-chromatic melody.) ↩
-
Prince Gvidon has two main leitmotifs in the opera, but only the one shown here participates in the melody line. The other one also appears in Flight of the Bumblebee but not within the melody line: it is the descending and ascending staccato line which appears several times in the accompaniment. ↩
-
The repeat is only found in the original opera score, not in the popular piano reduction. ↩
-
Speaking of speculation, here is a pretty big leap: Rimsky-Korsakov is known to have had synesthesia, associating colours with different keys. While there is no documented evidence of Rimsky-Korsakov’s associations with the minor keys, there are descriptions of his associations with the major keys. While I was unable to find the primary source describing Rimsky-Korsakov’s colour-key synesthesia, I do believe there to be a primary source in Russian, because several of the secondary sources use different translations of the colour names.
The parallel and relative major keys actually line up well with bumblebees. Flight of the Bumblebee is written in A minor, and modulates to D and G minor. In Rimsky-Korsakov’s classification, the parallel major keys, A, D, and G major, correspond to rose, yellow and gold, respectively. These colours evoke the imagery of a yellow-gold bumblebee flying to bright flowers. Additionally, the relative major keys of these minor keys—C major, F major, and Bb major—correspond to green and white, with no documented correspondance for Bb major. These associations, while interesting, are probably a coincidence, especially without evidence about his colour associations with the minor keys. ↩