Optimality in card shuffling
Many powerful minds have devoted countless decades to the academic study of card games. However, relatively little attention has been given to the best way to shuffle a deck of cards. There are several different methods that people have developed to shuffle cards:
- The riffle shuffle: The classic shuffling method. Cut the deck approximately in half. Take one half in each hand, and let the cards from both decks fall on top of one another.
- The overhand shuffle: Another very popular method. Hold the cards in one hand, and take the cards with your other hand, and let them fall on top.
- The Hindu shuffle: A method popular in India. It is a different style of performing an overhand shuffle.
- The pile shuffle: Create several sub-decks of cards, by placing cards one-by-one into a (potentially random) sub-deck. Then, combine the sub-decks together.
It has been claimed that seven, eight, or more riffle shuffles are necessary to obtain complete randomization. However, these studies assume that any difference in probability between a shuffled deck and a fully random permutation can be exploited by the players. This is an important model for casinos where large amounts of money are at stake, but for games between friends where perfect randomness is not needed, seven or eight shuffles in between hands causes a substantial delay in the game.
Thus, below I describe how many shuffles you need in practice instead of in theory. My evaluation looks for patterns and irregularities in hands that would be dealt. It accounts for three types of patterns—suits, ranks, and clusters/straights—by looking at the joint distribution of of these frequencies compared to a null distribution. (For instance, a six card hand containing four of one suit and two of another is highly unlikely.) I simulate a number of different shuffling methods and find the probability of obtaining the arrangements generated by these shuffles in a truly random deck.
Each of the shuffles starts with either fully ordered decks (i.e. a new deck of cards), or else with cards in an order representative of a specific card game. I compare these to a deck which started out fully randomized before the shuffle as a control, which is therefore guaranteed to be fully randomized after the shuffle. All shuffles should be compared to the randomized deck, i.e. the red line in the plots.

Card game deck patterns used in all figures which follow.
Riffle shuffle
The riffle shuffle is arguably the most popular shuffling method. The standard accepted mathematical model for the Riffle shuffle is called the Gilbert-Shannon-Reeds model (GSR model). (Yes, that’s Claude Shannon.) This model assumes that the shuffler is an expert and can dynamically adjust the rate at which cards are laid down from each hand during the shuffle. It states that the probability of putting down a card from either hand is proportional to the relative size of the deck in that hand. For example, if your left hand had 30 cards and your right hand had 10, you would have a 3/4 probability of the next card coming from your left hand.
Hesitant to accept this definition, I developed another model which includes a skill parameter \(\lambda\). High \(\lambda\) means that there is a low probability of two consecutive cards being dealt from the same hand, whereas low \(\lambda\) means there will be large bunches of cards from the same hand in the deck. This is motivated by the fact that, given the speed at which cards are shuffled, most people do not have the reaction time necessary to adjust the rate at which they let cards fall from either hand, and also by the fact that casino dealers come close to alternating cards from each hand.
In order to test these models, I collected data from my own shuffles to determine the most likely model. I found that my model was slightly more likely given the data, but if you account for the fact that my model has a parameter whereas the GSR model has none, the GSR model is a slightly better fit to the data.
Because they were close, I decided to test both cases, and also to vary the skill level \(\lambda\). I tested four cases: a novice shuffler (\(\lambda=0.3\)), an average shuffler (\(\lambda=0.45\), the best fit to my shuffling data), an expert shuffler (\(\lambda=0.8\)), and the ideal GSR case (which has no parameter).
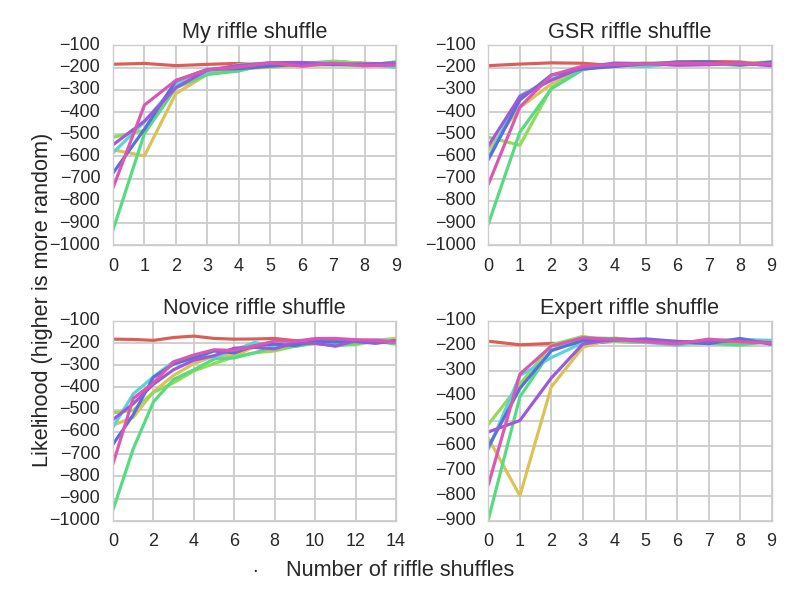
Effectiveness of riffle shuffles as a function of the number of consecutive shuffles.
As we can see, people comfortable with a riffle shuffle need approximately 4 shuffles in order to randomize the deck, which is approximately half of the theoretical recommendation. An average card player does not have any advantage over a professional casino dealer in this regard. Of course, if you’re not riffle shuffling very well, it will take far more shuffles to achieve the same degree of randomness.
Overhand/Hindu shuffle
The overhand shuffle is equivalent to dividing the deck into a number of sub-decks and then recombining those decks in reverse order. By watching several YouTube videos of people performing the overhand shuffle, there is a wide variety in the number of times people will divide the deck when performing the shuffle. Most people do it around 5 times, but some people consistently do more or fewer than this.
Here, we consider the cases of 5 cuts, 3 cuts, and 8 cuts, as these values covers the typical range of cuts.
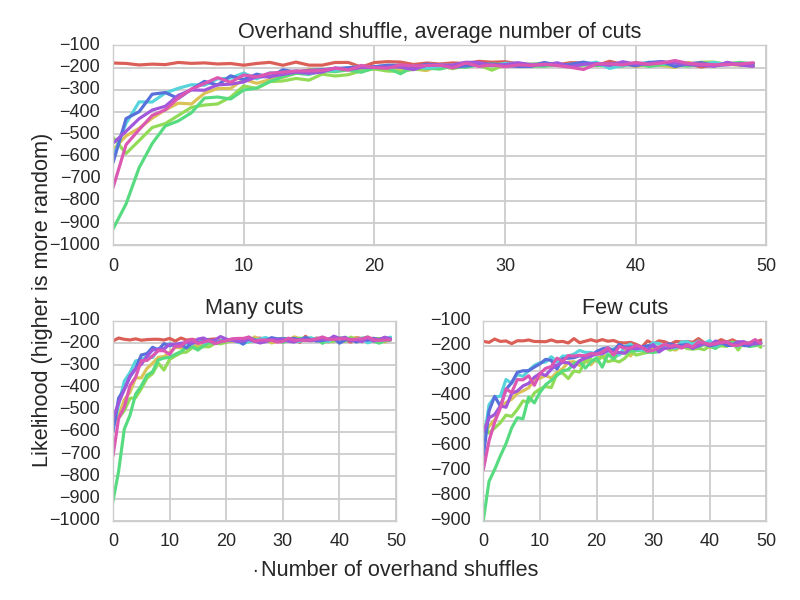
Effectiveness of overhand shuffles as a function of the number of consecutive shuffles.
It takes many more overhand shuffles to randomize the deck. Assuming an average number of cuts, it takes approximately 25 shuffles, which is 20-60 times less than the theoretical result. When you only cut the deck 3 times during an overhand shuffle, this number jumps to almost 40. Nevertheless, this goes against the theoretical finding, and suggests that the overhand shuffle is a valid and useful method, even if it is a bit more time consuming.
Pile shuffle
The pile shuffle has many variants. In the strict form, the shuffler deals all of the cards into some number of piles, and then stacks the cards on top of each other.
Clearly this strict form is both deterministic and highly patterned, and thus it is rather ineffective. Sometimes, people will add a slight bit of randomization by picking up the piles in a different order than they laid them down. More frequently, people will perform this deal by randomizing the order in which they lay down cards into the decks. Sometimes they will do so while keeping the decks approximately the same size, and sometimes they will disregard deck size. (However, note that people are notoriously bad at randomizing, so these should be considered the maximum limits of randomization rather than the method’s true amount of randomization.)
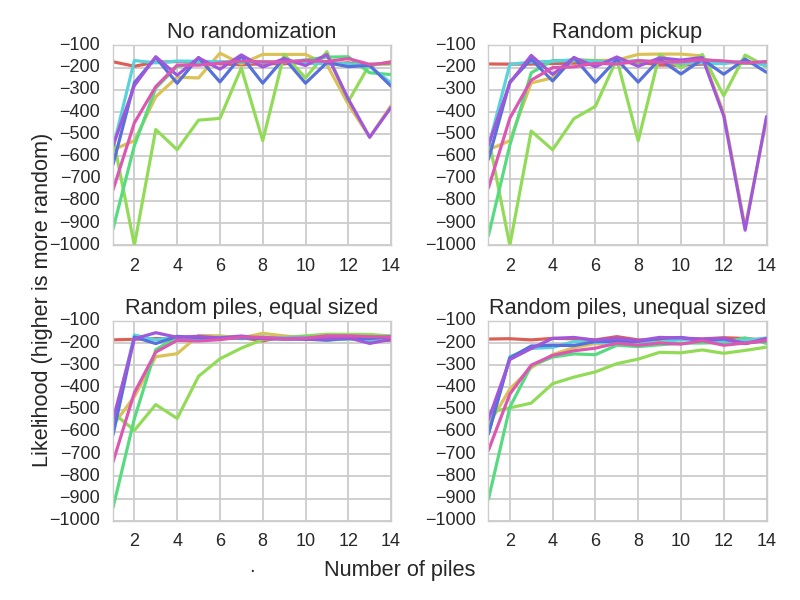
Effectiveness of pile shuffles as a function of the number of piles.
We see that pile shuffling is not very efficient when only performed once. The reason appears to be that this method does not randomize the ranks in the deck. If you started with an ordered deck, you can be nearly certain that if you pick up a 3, the next card will not be a 2. Most versions of pile shuffling are ineffective for this reason. The only version which works is the version which keeps the decks at an approximately similar size throughout the duration of the shuffle, while using at least eight decks. However, this also assumes that the shuffler is able to generate near-random numbers, which is impossible without either a random number generator or knowledge of strategies for generating random numbers without one.
Miscellaneous results
I simulated two styles of deals from the shuffled deck: one where the top 6 cards were taken from the deck, and one where there were 4 players, and 6 cards were dealt to each in a clockwise manner. Results were nearly identical for both cases, so only results for the former are included here.
I also simulated the mixed case which combines riffle shuffles and that overhand shuffles, with the hypothesis that adding a few overhand shuffles could reduce the number of riffle shuffles needed to randomize the deck. Unfortunately, this turned out to not be the case. Adding one or two overhand shuffles to different places in the riffle shuffle sequence was not able to reduce the number of riffle shuffles needed to randomize the deck.
If we assume that the riffle shuffle takes approximately 5 seconds to perform and the overhand shuffle takes 2 seconds to perform, it takes 40 seconds to randomize the deck using the overhand shuffle but 20 seconds to randomize it using the riffle shuffle. If we assume that four cards can be dealt per second and decks can be straightened and stacked at a rate of one per subpile, a suitable pile shuffle would take 21 seconds. However, this is also assuming suitable randomization, and thus, cards may not be as randomized as in the other methods.
There are other considerations in choosing the shuffling method as well; for instance, the overhand shuffle is considered to be less damaging to the cards than a riffle shuffle, which may bend the cards.
Summary
From this analysis, we have learned the following:
- The riffle shuffle is highly efficient, requiring only 4 shuffles in order to make a deck random for most practical purposes.
- When using 5 deck cuts in the overhand shuffle, about 25 shuffles are necessary to randomize the deck. While it takes longer to perform, it is equally as effective as 4 riffle shuffles after 25 iterations.
- 10 or more riffle shuffles may be required if the shuffler lacks experience.
- The pile shuffle should generally be avoided, unless using eight or more piles, distributing cards randomly, ensuring all piles are approximately the same size, and ideally finding a way to circumvent the limitations humans have in generating random numbers.
- Combining overhand shuffles with riffle shuffles does not increase randomization compared to just using riffle shuffles.